[译]算法_二叉树

（最大）二叉堆是一个维护着最大堆属性的完全二叉树。
最大堆用来实现高效的优先级队列PQ(Priority Queue)。

为集中精力讨论二叉堆本身，本教学中的最大二叉堆中不包含相同的数值。

完全二叉树的定义：除最下层，其它层组成满二叉树（每个节点上都有值），而最下层的节点都靠左排列不留空隙。

最大二叉堆属性：每个节点的父节点(除了根节点)，都比该节点大。

优先级队列：

1. Enqueue(x)，将新元素x放入队列(按照某种次序)
2. y = Dequeue()，将序列中优先级最大的值返回；若存在相同优先级的值，则返回最先插入的值，即退化到FIFO

最大二叉堆的高度 <= log N(二分)

完全二叉树可以高效的存储为数组，因为展开为数组之后，各节点之间没有空隙。为简化遍历操作，我们假设数组下标从1开始。

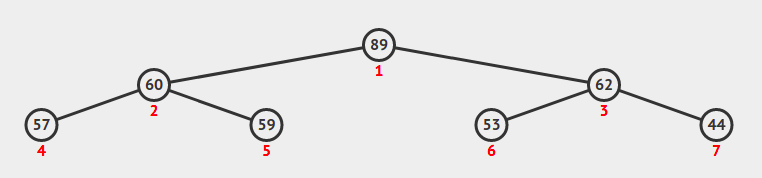
1. parent(i) = i>>1，例如8号节点的父节点为4号则parent(8) = 8>>1 = 4
2. left(i) = i<<1
3. right(i) = (i<<1) + 1

本教学中会介绍一下（最大）二叉堆的操作：

1. Insert(v) O(log N)
2. ExtractMax() O(log N)
3. Create(A) O(N log N)版本
4. Create(A) O(N)版本
5. HeapSort() O(N log N)

Inset(v)

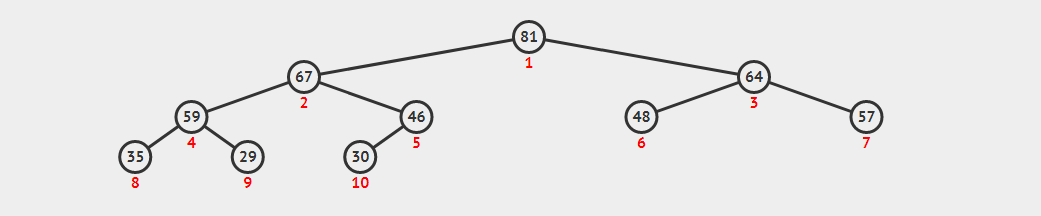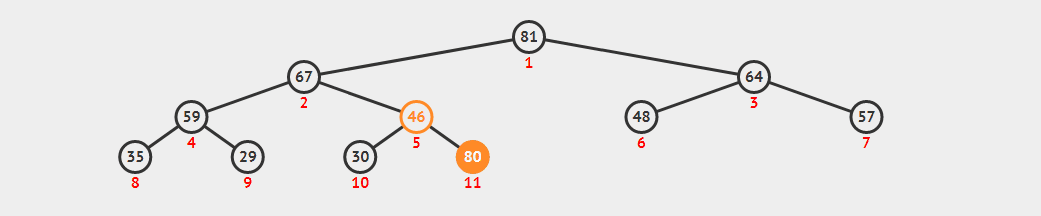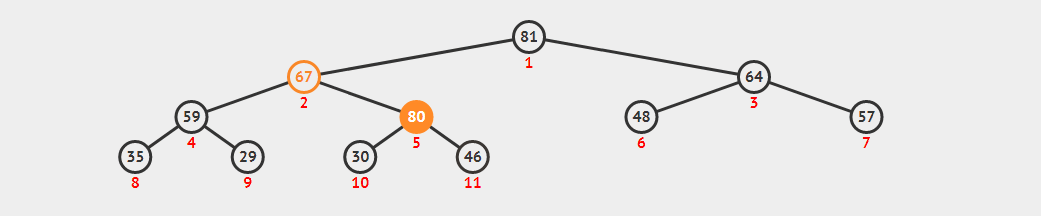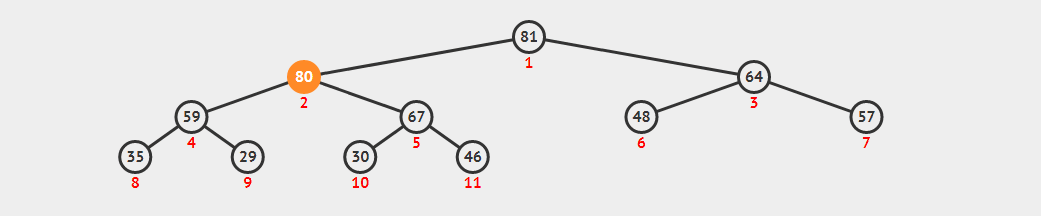
插入操作只能在最末尾的位置进行，这是为来保证二叉树的完全二叉树属性。但此时也可能会破坏最大堆属性，因此插入点可能需要向上移动。这个操作称之为ShitUp或BubbleUp或IncreaseKey。

ExtractMax

删除堆顶数据，然后将最末尾数据移动到堆顶，此时会破坏最大堆结构，因此需要向下调整。称之为ShiftDown或BubbleDown或Heapify操作。
在向下调整时，总是和较大的子节点交换。

PQ - 优先级队列

到此，有了Insert(v)和ExtractMax()操作，我们实现了优先级队列。

前中后序遍历

package main

import (
    "fmt"
    "github.com/straysh/basis_go/datastructure"
)

func main() {
    n1 := &datastructure.BTNode{Data: 81}
    n2 := &datastructure.BTNode{Data: 80}
    n3 := &datastructure.BTNode{Data: 64}
    n4 := &datastructure.BTNode{Data: 59}
    n5 := &datastructure.BTNode{Data: 67}
    n6 := &datastructure.BTNode{Data: 48}
    n7 := &datastructure.BTNode{Data: 57}
    n8 := &datastructure.BTNode{Data: 35}
    n9 := &datastructure.BTNode{Data: 29}
    n10 := &datastructure.BTNode{Data: 30}
    n11 := &datastructure.BTNode{Data: 46}

    n1.Left = n2; n1.Right = n3
    n2.Left = n4; n2.Right = n5
    n3.Left = n6; n3.Right = n7
    n4.Left = n8; n4.Right = n9
    n5.Left = n10;n5.Right = n11

    //前序遍历
    preOrder(n1)
}

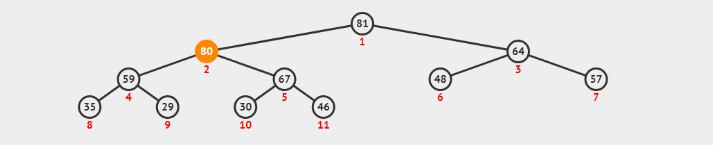
递归法 - 前序遍历

func preOrder(node *datastructure.BTNode) {
    if node==nil {
        return
    }
    fmt.Printf("%d ", node.Data)
    preOrder(node.Left)
    preOrder(node.Right)
}
//输出: 81 80 59 35 29 67 30 46 64 48 57

递归法 - 中序遍历

func inOrder(node *datastructure.BTNode) {
    if node==nil {
        return
    }
    inOrder(node.Left)
    fmt.Printf("%d ", node.Data)
    inOrder(node.Right)
}
//输出: 35 59 29 80 30 67 46 81 48 64 57

递归法 - 后序遍历

func postOrder(node *datastructure.BTNode) {
    if node==nil {
        return
    }
    postOrder(node.Left)
    postOrder(node.Right)
    fmt.Printf("%d ", node.Data)
}
//输出: 35 29 59 30 46 67 80 48 57 64 81

深度优先(DSF) - 前序遍历

func dsf(node *datastructure.BTNode) {
    stack := datastructure.NewStackBT(11)
    stack.Push(node)

    for ;stack.Size() != 0; {
        item := stack.Pop()
        fmt.Printf("%d ", item.Data)
        if item.Right!=nil {
            stack.Push(item.Right)
        }
        if item.Left!=nil{
            stack.Push(item.Left)
        }
    }
}
//输出: 81 80 59 35 29 67 30 46 64 48 57

深度优先(DSF) - 中序遍历

func dsfInOrder(node *datastructure.BTNode) {
    stack := datastructure.NewStackBT(11)
    p := node

    for ;p!=nil; {
        if p.Left != nil {
            stack.Push(p)
            p = p.Left
        } else {
            fmt.Printf("%d ", p.Data)
            p = p.Right
            for ;p==nil && stack.Size()>0; {
                p = stack.Pop()
                fmt.Printf("%d ", p.Data)
                p = p.Right
            }
        }
    }
}
输出: 35 59 29 80 30 67 46 81 48 64 57

深度优先(DSF) - 后序遍历

//todo

广度优先(BSF) - 按层遍历

func bsf(node *datastructure.BTNode) {
    queue := datastructure.NewQueueBT(11)
    queue.Enqueue(node)

    for ;queue.Size()>0; {
        p := queue.Dequeue()
        fmt.Printf("%d ", p.Data)

        if p.Left!=nil {
            queue.Enqueue(p.Left)
        }
        if p.Right!=nil {
            queue.Enqueue(p.Right)
        }
    }
}

求树的高度

func btHeight(node *datastructure.BTNode) int {
    if node == nil {
        return 0
    }

    return max(btHeight(node.Left), btHeight(node.Right)) + 1
}