[译]算法_非基于比较的排序算法

非基于比较的排序算法 - O(N)

1. 计数排序
2. 基数排序

由于不比较元素对，它们比基于比较的排序最优解O(N log N)还要快。

众所周知（本教学中未证明），基于比较的排序算法，最快也是O(N log N)。因此，任何最快情况下复杂度是O(N log N)的算法，例如归并排序，被认为是最佳的。

计数排序

假设：待排序序列是少量整型数值，我们统计各个数值出现的次数，然后迭代数值范围来输出正序的数组。

例如，下例中所有数均在[1..9]中，我们先计算1出现的次数，2出现的次数…9出现的次数，然后迭代1-9并按出现次数x打印数值。

统计数值频率是O(N)，打印正序数列是O(N+K)，其中k是数值取值范围。当k较小时，即O(N)。

若k极大，则受内存限制统计频率将不可行。

基数排序

假设：待排序的元素是大范围但小数值的整数，我们可以在基数排序中利用计数排序的思想来达到线性的时间复杂度。

在基数排序中，我们将每个元素看到是包含w位的字符串（不足w位的元素，左侧补零）。

从最低位（最右侧）到最高位（最左侧），逐位按计数排序方法将数据源排序，知道最高位排序完成，则正序。

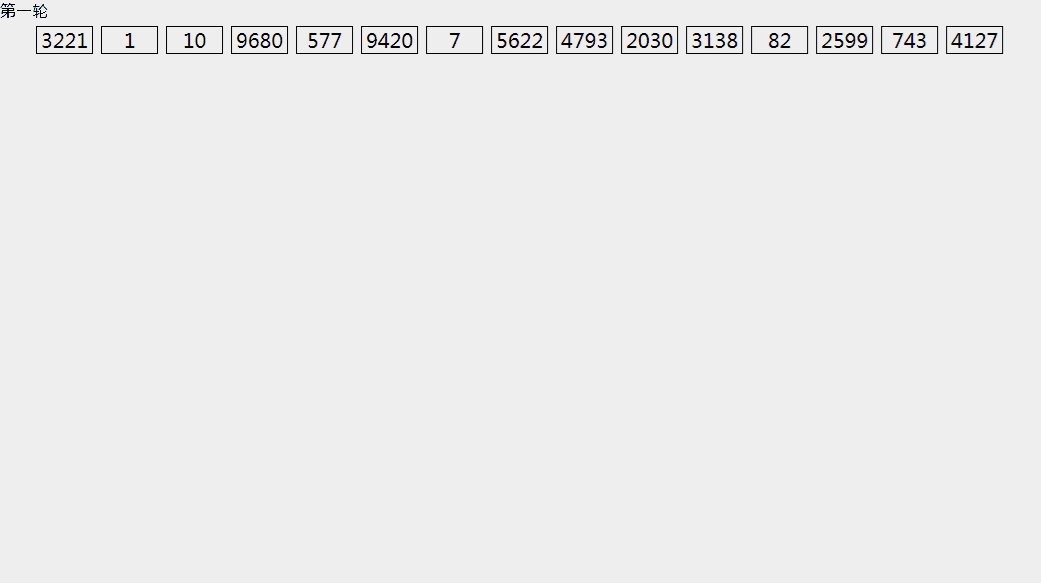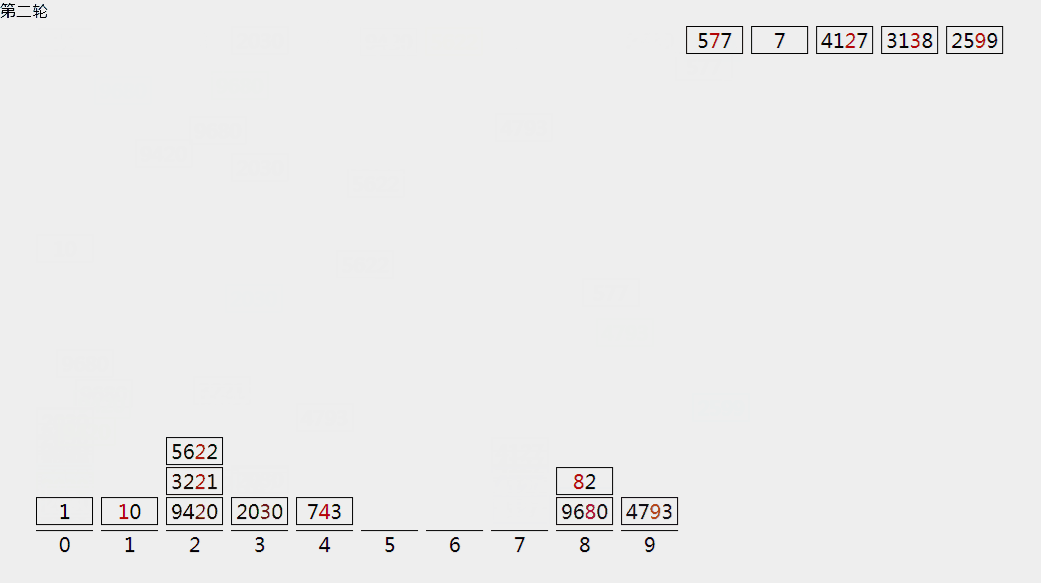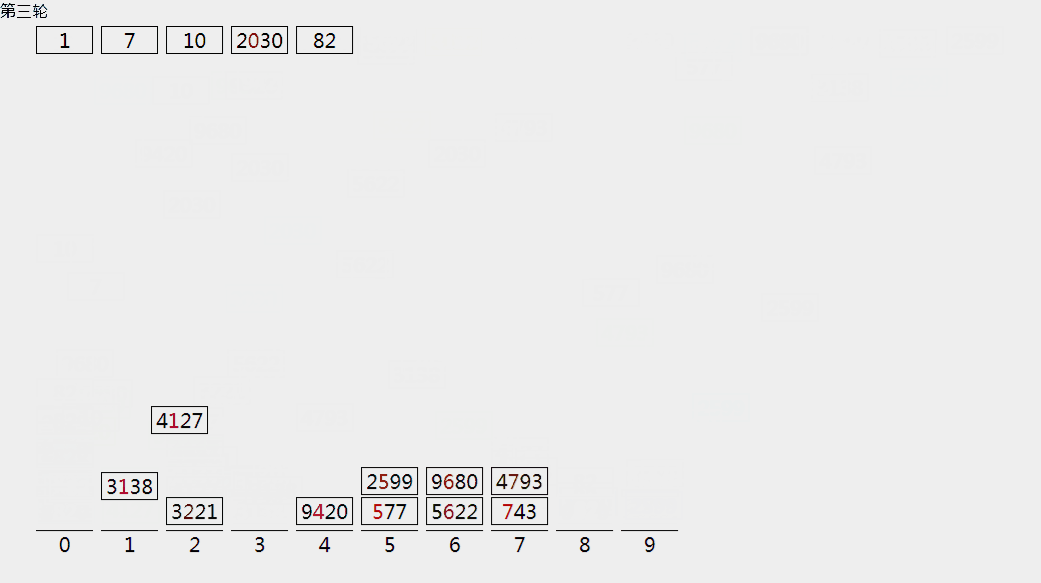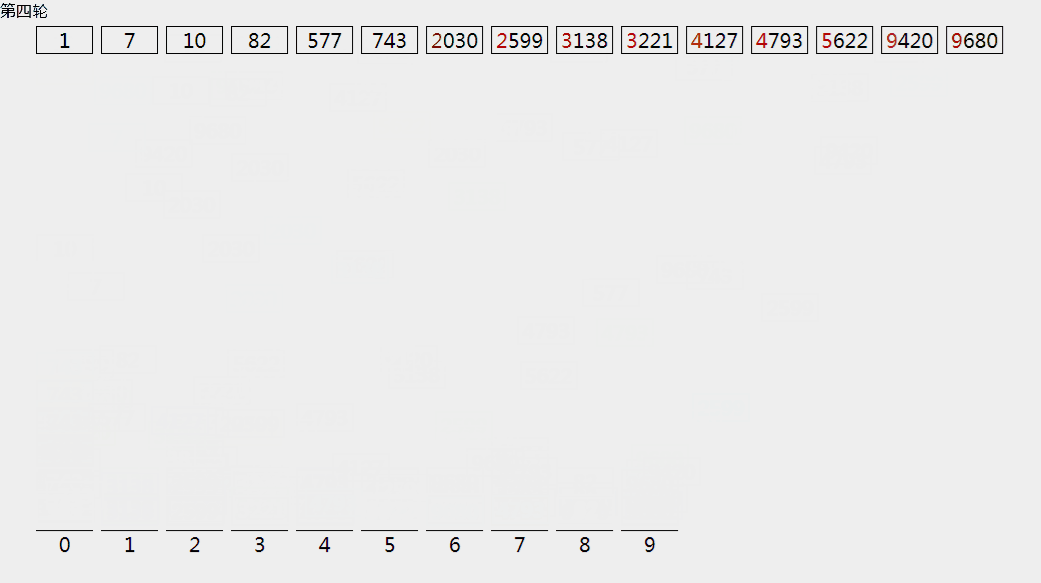
我们只需要O(w * (N+K))，本例中w=4,K=10。

讨论

排序算法的特点不仅仅是比较、非比较、递归、迭代的区别，
下面讨论一下原地排序/非原地排序，稳定排序/非稳定排序。

原地排序

原地排序指的是在排序时，只需要有限额外内存的排序算法。即可以有少量，有数的额外变量，但不能有不确定的变量数特别是这个数的大小依赖与数据源的大小N。

归并排序在子步骤合并阶段需要额外的空间，不是原地排序算法。

• 冒泡、选择、插入是原地排序
• 快速排序，是原地排序
• 归并排序，不是原地排序
• 计数排序，不是原地排序
• 基数排序，不是原地排序

稳定排序

当排序完成之后，值相同的元素的相对为止保持不变的算法，称之为稳定排序算法。

讨论：有哪些稳定排序算法？