[译]算法_排序_基于比较的排序

2020-02-12 博文 Algorithm, Golang, Translation 评论

基于比较的算法复杂度`O(N²)`

我们讨论三种基于比较的算法：

冒泡
选择
插入

因为这些算法需要比较两个元素以决定是否交换位置，故称基于比较的算法。

这三种算法最容易实现，但不是最高效的。其时间复杂度是O(N²)。

冒泡算法

给定数组N个元素，冒泡算法会：

比较一对邻近的元素(a,b)。
当这对元素无序时，交换他们。（此是当a>b时）。
重复步骤1，步骤2直到数组尾。
此时，最大元素会是最后一个元素。然后令N=N-1，并重复步骤1直到N=1。

[29, 10, 14, 37, 14]，冒泡的动画示意如下：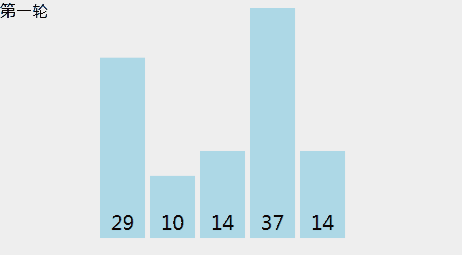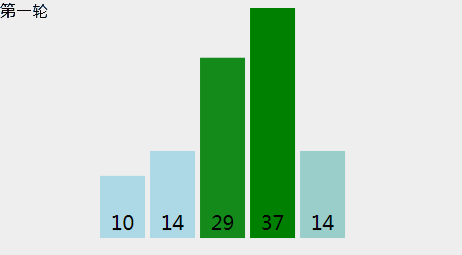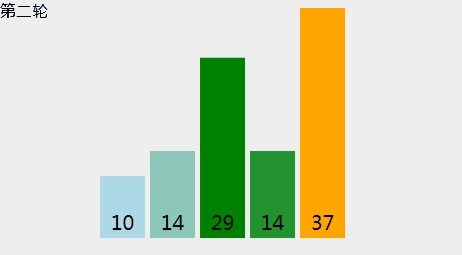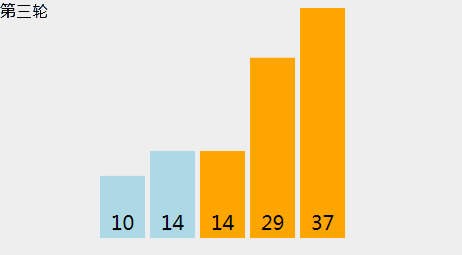
Sorting_BUB

冒泡排序的分析

比较和交换需要常量时间，我们取c。

标准冒泡算法中有两层循环。
外层循环需要迭代N次。
但内层循环迭代的次数会越来越少：

当i=0, N-1次迭代 - 比较和(可能的)交换
当i=1，N-2次迭代
当i=2，N-3次迭代
…
当N=N-2，1次迭代
当N=N-1，0次迭代

因此总共需要的迭代次数= (N-1) + (N-2) + ... + 1 + 0 = N*(N-1)/2。

总共花费的时间 = c * N*(N-1)/2 = O(N²)。

func BUB(a []int) {
    N := len(a)

    for i := 0; i < N; i++ {
        allSorted := true
        for j := 0; j < N-i-1; j++ {
            if a[j] > a[j+1] {
                a[j],a[j+1] = a[j+1],a[j]
                allSorted = false
            }
        }
        if allSorted {
            return
        }
    }
}

冒泡改进 - 提前终止

冒泡排序并不高效，因为它是O(N²)的时间复杂度。

但若能提前终止(多余的)冒泡进程，时间复杂度可以提高到O(1)。

例：[3, 6, 11, 25, 39]。改进方法很简单：若内层循环没有发生交换，那么整个序列已经是正序的，此时可以终止冒泡进程。

讨论：这个改进让冒泡排序在一般情况下更快了，但无法改变其时间复杂度O(N²)的时间，为啥？

选择排序

令数组大小为N，L=0，选择排序步骤如下：

找到元素[L .. N-1]中最小元素X的位置。
将X元素和位置L的元素交换。
L++，并重复步骤1。

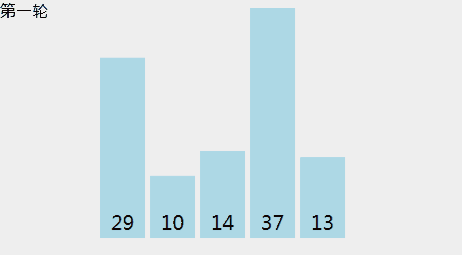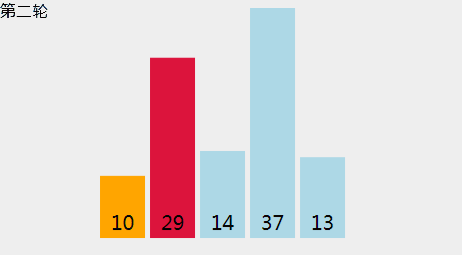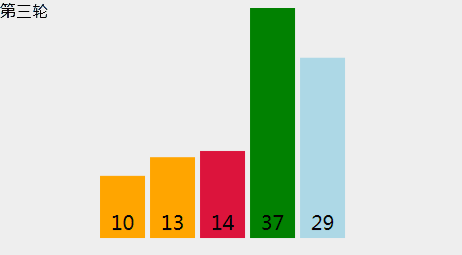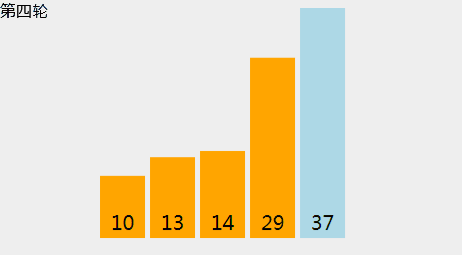
Sorting_SEL

func SEL(a []int) {
    N := len(a)

    for L := 0; L < N-1; L++ {
        X := minElements(a, L)
        a[X],a[L] = a[L],a[X]
    }
}
func minElements(a []int, offset int) int {
    min := offset
    for i:=offset;i<len(a);i++{
        if a[i] < a[min] {
            min = i
        }
    }

    return min
}

当然，也可以更改算法为找最大数并交换。

时间复杂度和冒泡是一样的O(N²)。

插入排序

插入排序有点像给手上的扑克牌排序的过程。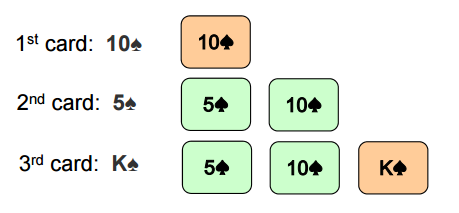
inserting_sort_example

手上拿第一张牌。
拿到下一张牌，在目前有序的牌中找到正确的位置并插入新牌。
重复上述步骤直到所有牌结束。

func INS(a []int) {
    N := len(a)

    for i := 1; i < N; i++ {
        for j := i; j > 0; j-- {
            if a[j] < a[j-1] {
                a[j],a[j-1] = a[j-1],a[j]
            }
        }
    }
}

func INS(a []int) {
    N := len(a)

    for i := 1; i < N; i++ { // O(N)
        x := a[i]   // 带插入的牌
        j := i - 1  // 正序部分的最高索引
        for ; j >= 0 && a[j] > x; j-- {  //最好O(1)，最坏O(N)
            a[j+1] = a[j]  // 给x腾出空间
        }
        a[j+1] = x // j+1是要插入的位置
    }
}

分析插入排序

外层循坏需要N-1次迭代。

但内层循环的次数：

最好的情况下，只需要一次比较a[j] > x就能确定是正序的，因此是O(1)。
最坏的情况下，数组是逆序的，这样每次迭代a[j] > x都是true，每次都需要迭代整个内层循环，时间复杂度是O(N)。

因此，最好情况是O(1)，最坏情况是O(N²)。

基于比较的 `O(N log N)` 的排序

归并排序
快速排序和随机快速排序

这些算法通常使用递归实现，采用分治思想，归并排序和随机快速排序都是O(N log N)。

快速排序的非随机版本是O(N²)的。

归并排序

令数组大小为N，归并排序步骤如下：

将两个元素合并到一个正序的（仅含这两个元素）数组中。
将两个上述数组合并到一个正序的（现在含有四个元素）数组中。
最终：将两个各含有N/2的数组合并到一个数组中，则数组正序。

这仅是一个概要，我们还需要讨论更多细节才能应用归并排序

归并排序中复杂度`O(N)`的子步骤

我们将归并排序拆开讨论，先讨论复杂度为O(N)的子步骤。

令数组A大小为N₁，数组B大小为N₂，我们很容易将之合并为一个正序的大小N=N₁+N₂的数组

只需要比较数组的第一个元素，将较小的数组元素全部放到另一个数组之前。这个O(N)的操作需要额外的数组来存储数据。

Sorting_MER

void merge(int a[], int low, int mid, int high) {
  // subarray1 = a[low..mid], subarray2 = a[mid+1..high], both sorted
  int N = high-low+1;
  int b[N]; // discuss: why do we need a temporary array b?
  int left = low, right = mid+1, bIdx = 0;
  while (left <= mid && right <= high) // the merging
    b[bIdx++] = (a[left] <= a[right]) ? a[left++] : a[right++];
  while (left <= mid) b[bIdx++] = a[left++]; // leftover, if any
  while (right <= high) b[bIdx++] = a[right++]; // leftover, if any
  for (int k = 0; k < N; k++) a[low+k] = b[k]; // copy back
}

Golang实现：

func merge(a []int, low, mid, high int) {
    N := high - low + 1
    left := low
    right := mid + 1
    idx := 0
    b := make([]int, N, N)
    for ; left <= mid && right <= high; {
        if a[left] <= a[right] {
            b[idx] = a[left]
            left = left + 1
        } else {
            b[idx] = a[right]
            right = right + 1
        }
        idx = idx + 1
    }
    if left <= mid {
        b[idx] = a[left]
        left = left + 1
        idx = idx + 1
    }
    if right <= high {
        b[idx] = a[right]
        right = right + 1
        idx = idx + 1
    }

    for i := 0; i < N; i++ {
        a[low+i] = b[i]
    }
}

分治思想

分治法 - Divide and Conquer简写作D&C。

Divide step：将一个问题分解成小的问题，然后递归的解决小的问题。
Conquer step：将解决了的小问题合并起来，还原为原始问题的解。

归并算法的分治思想

归并算法是分治的一个应用。

divide step：将数组分为两半，然后递归的对两个数组分派归并排序。

conquer step：将结果集合并成解，这一步骤的工作量最大。

void mergeSort(int a[], int low, int high) {
  // the array to be sorted is a[low..high]
  if (low < high) { // base case: low >= high (0 or 1 item)
    int mid = (low+high) / 2;    
    mergeSort(a, low  , mid ); // divide into two halves
    mergeSort(a, mid+1, high); // then recursively sort them
    merge(a, low, mid, high); // conquer: the merge subroutine
  }
}

Golang实现：

func MER(a []int, low, high int) {
    if low < high {
        mid := (low + high) / 2
        MER(a, low, mid)
        MER(a, mid+1, high)
        merge(a, low, mid, high)
    }
}

归并排序时间复杂度分析

归并排序中merge的复杂度是O(N)的，那么merge执行的次数决定了最终的时间复杂度。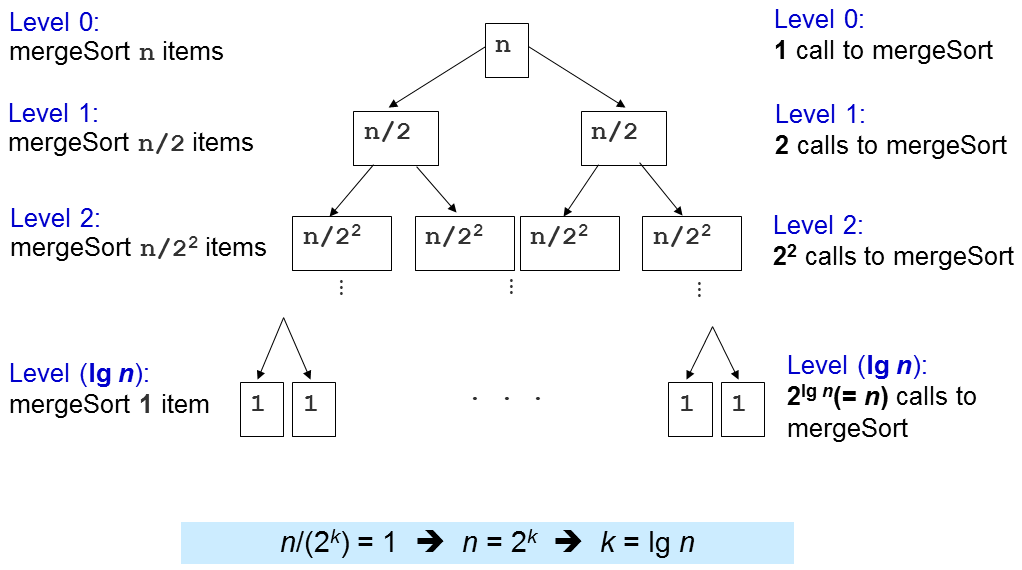
merge

可以看到k=lg N，忽略常数，我们记归并排序的时间复杂度为O(N log N)。

归并排序的优缺点

首先，最重要的一点是，归并排序的时间复杂度稳定的是O(N log N)，不受数据源的影响。没有任何的测试用例，不论数据源的大小，都不能是归并排序的时间超过O(N log N)。

目前为止，我们讨论过的算法中，归并排序是最适合处理大规模数据的算法。

归并排序是稳定排序算法，为啥？

当然，归并排序也有其劣势。

从头开始实现归并排序并不是很容易。
在合并阶段，需要额外的存储空间。因此内存利用率不高，也不是原地排序算法。

对归并排序的优化你可以参考这里

快速排序算法

快速排序也是分治法的应用。

Divide step：选择一个元素p，即pivot。
将数组a[i..j]分为三个部分：a[i..m-1], a[m], a[m=1..j]。
a[i..m-1]包含比p小的元素。
a[m]即pivot，m是p在数据源a中的索引。
a[m+1..j]包含了大于等于p的元素。
然后递归的重复上述步骤。

Conquer step：额，啥也不用做…

与归并排序对比，你会发现它的D&C步骤刚好相反。

分析快速排序

还是查分开讨论，先讨论复杂度为O(N)的子步骤。

为了分割a[i..j]，我们先找到一个pivotp = a[i]。
剩下的a[i+1..j]将被分割为三个部分：

S1=a[i+1..m]，元素都 < P。
S2=a[m+1..k-1]，元素都 ≥ p。
未知部分 = a[k..j]，其他元素待分配到S1 或 S2。

讨论：为什么选择p=a[i]，有没有其他选择？
硬核讨论：若每次都将==p的元素放在S2里合适吗？

起初，S1和S2都是空的，所有的元素除了p=pivot都在未知区域中。
对于每一个在位置区域的元素a[k]，将a[k]与p比较：

a[k] ≥ p，将a[k]放入S2。

a[k] < p，将a[k]放入S1。
最后交换a[i]和a[m]，即将p放在S1和S2的中间。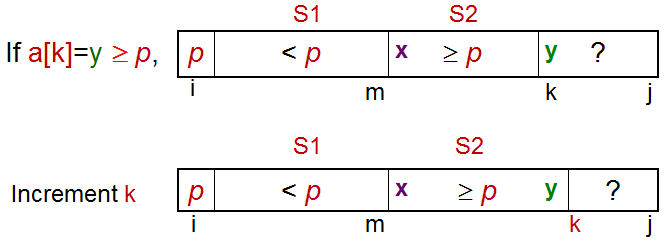
partition1

代码如下：

int partition(int a[], int i, int j) {
  int p = a[i]; // p is the pivot
  int m = i; // S1 and S2 are initially empty
  for (int k = i+1; k <= j; k++) { // explore the unknown region
    if (a[k] < p) { // case 2
      m++;
      swap(a[k], a[m]); // C++ STL algorithm std::swap
    } // notice that we do nothing in case 1: a[k] >= p
  }
  swap(a[i], a[m]); // final step, swap pivot with a[m]
  return m; // return the index of pivot
}

void quickSort(int a[], int low, int high) {
  if (low < high) {
    int m = partition(a, low, high); // O(N)
    // a[low..high] ~> a[low..m–1], pivot, a[m+1..high]
    quickSort(a, low, m-1); // recursively sort left subarray
    // a[m] = pivot is already sorted after partition
    quickSort(a, m+1, high); // then sort right subarray
  }
}

Golang实现：

func QUI(a []int, low, high int) {
    if low < high {
        pivot := partition(a, low, high)
        QUI(a, low, pivot-1)
        QUI(a, pivot+1, high)
    }
}
func partition(a []int, i, j int) int {
    p := a[i]
    m := i

    for k := i + 1; k <= j; k++ {
        if a[k] < p {
            m++
            a[k],a[m] = a[m],a[k]
        }
    }
    a[i],a[m] = a[m],a[i]
    return m
}

快速排序的时间复杂度分析

partition操作只有一个循环，复杂度是O(N)。

那么快速排序的时间复杂度取决于partition执行的次数。

最坏情况下，当数据源是升序的，经过一轮后，S1是空的，S2包含除了pivot外其他元素。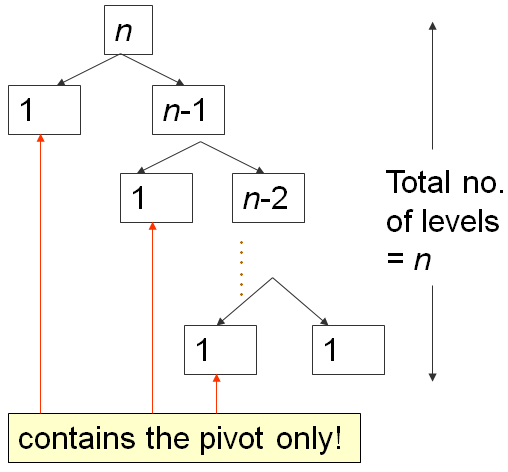
qsort_worstcase
一共需要N轮循环，所以时间复杂度是O(N²)。

而最好情况下，每一次pivot都将数据源分割为两半，一共需要log N次。
因此复杂度是O(N log N)。

随机快速排序 - O(N log N)

It will take about 1 hour lecture to properly explain why this randomized version of Quick Sort has expected time complexity of O(N log N) on any input array of N elements.

In this e-Lecture, we will assume that it is true.

If you need non formal explanation: Just imagine that on randomized version of Quick Sort that randomizes the pivot selection, we will not always get extremely bad split of 0 (empty), 1 (pivot), and N-1 other items. This combination of lucky (half-pivot-half), somewhat lucky, somewhat unlucky, and extremely unlucky (empty, pivot, the rest) yields an average time complexity of O(N log N).

Discussion: Actually the phrase “any input array” above is not fully true. There is actually a way to make the randomized version of Quick Sort as currently presented in this VisuAlgo page still runs in O(N2). How?

本文链接： https://straysh.github.life/2020/02/12/%E7%AE%97%E6%B3%95-%E6%8E%92%E5%BA%8F-%E5%9F%BA%E4%BA%8E%E6%AF%94%E8%BE%83%E7%9A%84%E6%8E%92%E5%BA%8F/

版权声明： 本博客所有文章除特别声明外，均采用 CC BY 4.0 CN协议许可协议。转载请注明出处！

Straysh野生程序猿

野生程序猿 & 猫奴。

[译]算法_排序_基于比较的排序

基于比较的算法 复杂度O(N²)

冒泡算法

冒泡排序的分析

冒泡改进 - 提前终止

选择排序

插入排序

分析插入排序

基于比较的 O(N log N) 的排序

归并排序

归并排序中复杂度O(N)的子步骤

分治思想

归并算法的分治思想

归并排序时间复杂度分析

归并排序的优缺点

快速排序算法

分析快速排序

快速排序的时间复杂度分析

随机快速排序 - O(N log N)

Straysh野生程序猿

基于比较的算法复杂度`O(N²)`

基于比较的 `O(N log N)` 的排序

归并排序中复杂度`O(N)`的子步骤