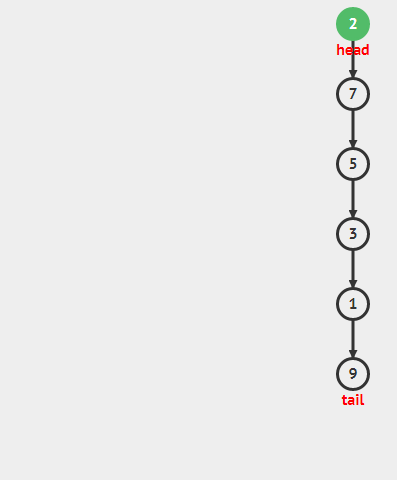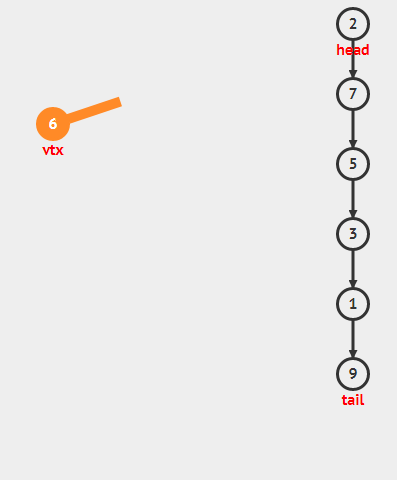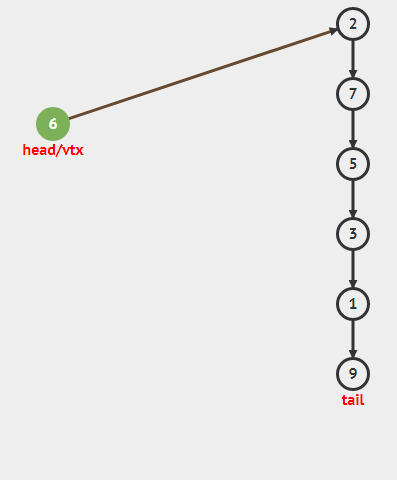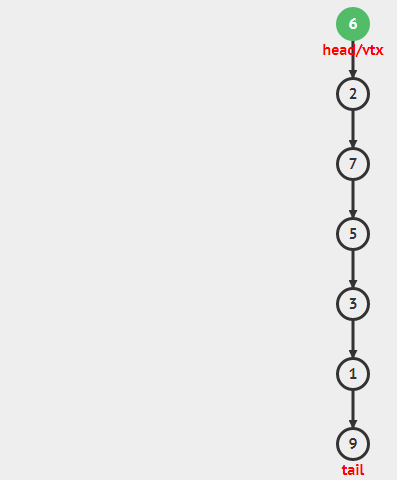
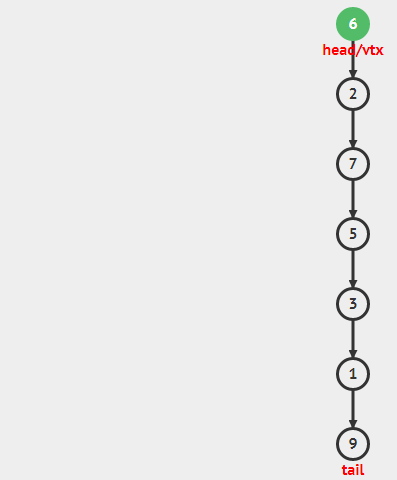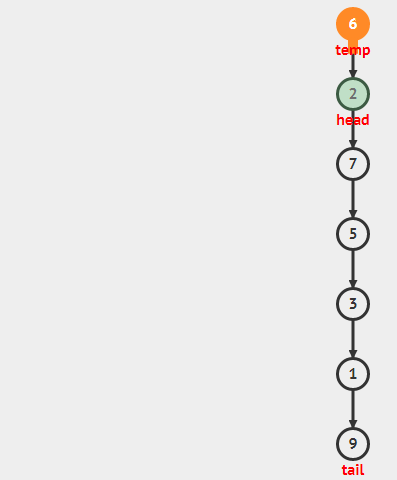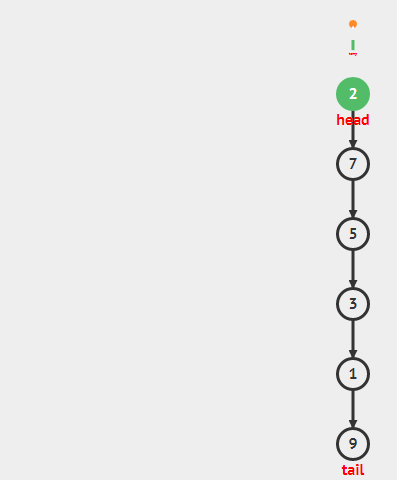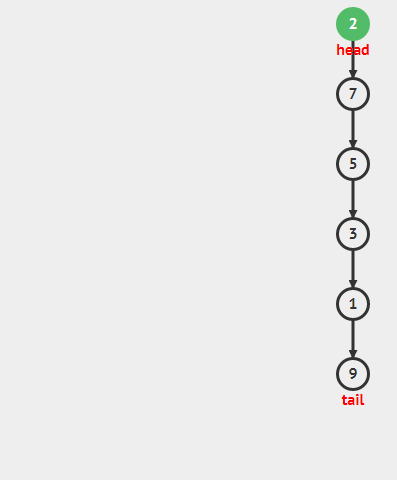
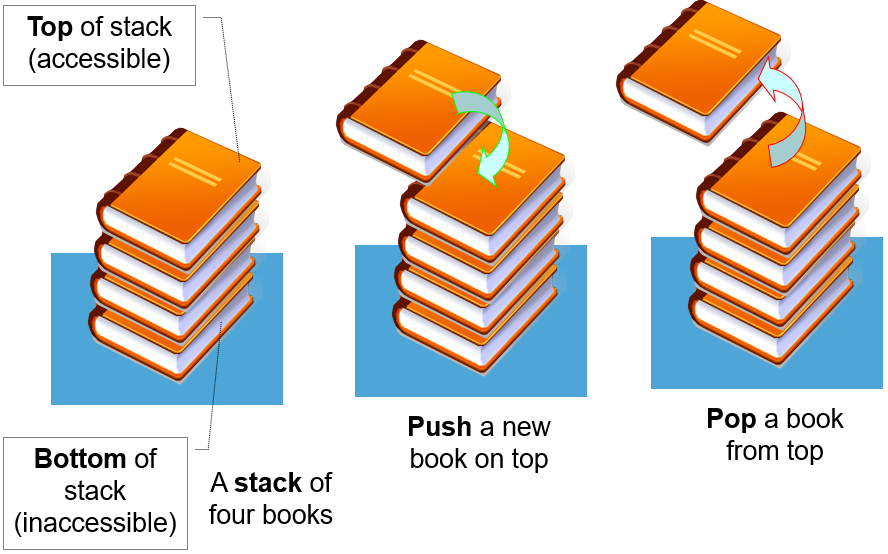
Stack栈是一种数据结构,它要求只能从顶部增加元素即push,只能从顶部移除元素即pop。亦即Last-In-First-out(LIFO)。
The Design Choice 栈的设计宗旨
在多数实现中,包括本教学中,栈是使用受保护的链表(连续的)来实现的,我们只能在顶部访问元素,push元素到顶部(头部插入),从头部pop元素出来(头部移除)。所有操作都是O(1)的。
讨论:能否使用变长数组来实现高效的栈结构?
栈的应用
教科书上,栈有一些典型的应用:
- Bracket Matching 括号匹配。
- Postfix Calculator 后缀计算器?
- A few other interesting applications that are not shown for pedagogical purposes.
Bracket Matching 括号匹配问题
数学表达式可以很复杂,例如:{[x+2]^(2+5)-2}*(y+5)。
括号匹配问题是检查表达式中的括号是不是成对的,(和),[和],{和}。
Golang实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| func checkBracketMatching(input string) bool {
stack := NewStack()
for i := 0; i < len(input); i++ {
c := fmt.Sprintf("%c", input[i])
switch c {
case "(", "[", "{":
stack.Push(c)
case ")":
if stack.Pop() != "(" {
return false
}
case "]":
if stack.Pop() != "[" {
return false
}
case "}":
if stack.Pop() != "{" {
return false
}
}
}
return stack.size == 0
}
|
Calculating Postfix Expression 后缀表达式的计算
后缀表达式用数学语言描述格式如下:data1 data2 op,与之对应的是更易理解中缀表达式:data1 op data2。
例:表达式2 3 + 4 * = (2+3) * 4。
在后缀表达式中,我们不需要括号辅助。
Golang实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| func postfixExpression() {
input := "2 3 + 4 *"
stack := NewStack()
for i := len(input) - 1; i >= 0; i-- {
c := fmt.Sprintf("%c", input[i])
if c != " " {
stack.Push(c)
}
}
fmt.Println(stack)
for ; stack.size > 1; {
data1 := stack.Pop()
data2 := stack.Pop()
d1, _ := strconv.Atoi(data1)
d2, _ := strconv.Atoi(data2)
op := stack.Pop()
temp := 0
if op == "+" {
temp = d1 + d2
} else if op == "-" {
temp = d1 - d2
} else if op == "*" {
temp = d1 * d2
} else if op == "/" {
temp = d1 / d2
}
stack.Push(strconv.Itoa(temp))
}
fmt.Printf("result:%s", stack.Pop())
}
|