[译]数据结构_链表

LL,Stack,Queue,DLL,Deque

链表（Linked List）是一种数据结构，它由一组节点组成，它们作为一个整体表示一个序列。最简单的情形下，每一个节点由一个值data和指向下序列中一节点的引用link组成。

在链表中查找数77

链表及其变体是用来实现列表（List）、栈（Stack）、Queue（队列）、Deque ADTs¹（双端队列）的底层数据结构。
Linked List and its variations are used as underlying data structure to implement List, Stack, Queue, and Deque ADTs

下面我们会讨论链表（只包含一个next指针）和它的两个变体：Stack和Queue，还会讨论Doubly Linked List（DLL）（双向链表）（包含next指针和previous指针），及其变体：Deque。

动机

链表这个数据结构通常会在大学本科阶段学习，有以下几个原因：

1. 它是一个简单的线性数据结构。
2. 作为一个抽象数据类型的列表，它有一系列的应用，例如学生列表，事件列表，任职列表等等（尽管有其他更多高级数据结构能做到同样(甚至更好)）或者作为栈/队列/双端队列的抽象数据类型。
3. 它有一些有趣的边界用例，指出了数据结构的良好实现的必要。
4. 它包含多种自定义的选项，因此特别适合使用OOP Programming面向对象编程来实现。

List ADT

List（列表）是一个有序数据序列 {a₀, a₁, …, a_N-2, a_N-1}
通常的List ADT（列表抽象数据类型）的操作有：
0. get(i) - 或许是个简单的操作，返回 a_i（基于0的索引）。

1. search(v) - 判断值v在列表中存在(并返回其位置/索引) 或不存在（通常返回索引-1）
2. insert(i,v) - 在列表的位置/索引i处插入值v，即将从位置[i+1 .. N-1]的元素均向右移动一个位置来生成一个空穴存放值v。
3. remove(i) - 将列表中位置i的值移除。即将位置[i+1 .. N-1]的元素均向左移动一个位置来消除空穴。

讨论：若我们需要在列表中移除值v呢？

数组的实现 - Part 1

（紧凑的）Array（数组）是实现List ADT的一个良好候选方式，因为它是处理数据集合的简单结构。

当我们说紧凑数组，我们指的是没有空穴的数组，举例：假设数组中有N个元素（数组的容量是M， M ≥ N），那么只有位置[0,N-1]被占用，其他位置[N, M-1]都是空的。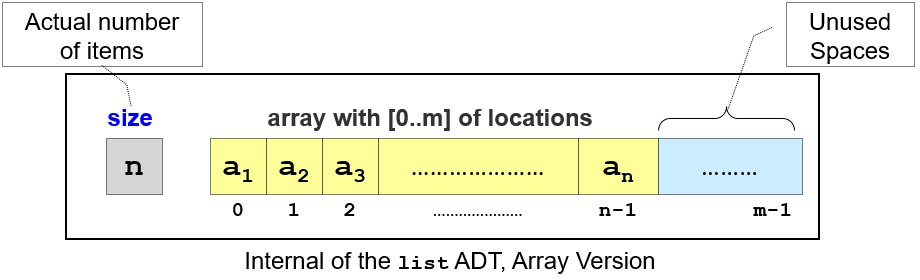

数组的实现 - Part 2

紧凑数组命名为A，下标范围[0 .. N-1]填充了数据。

1. get(i)返回元素A[i]。当数组是非紧凑的，这个简单的操作也会无必要的复杂。(This simple operation will be unnecessarily complicated if the array is not compact.)
2. search(v)我们逐项的遍历索引i（i∈[0 .. N-1]），检查A[i]==v。因为若值v存在，那么它的索引必将落在[0 .. N-1]中。
3. insert(i,v)我们将元素∈[i .. N-1]集合，顺序移动到∈[i+1 .. N]（向右移动）并设置A[i] = v。既要将v插入正确的索引i，还要确保数组是紧凑的。
4. remove(i)我们将元素∈[i+1 .. N-1]集合，顺序移动到∈[i .. N-2]（向左移动）将旧的A[i]覆盖掉。即能保持紧凑。

Time Complexity Summary 时间复杂性概要

1. get(i)非常快： 只需要一次查询，是O(1)。
2. search(v)
   • 最好的情况，值v是第一个元素，即O(1)。
   • 最坏的情况，值v不存在，我们需要O(N)复杂度的扫描才能确定这个实事。
3. insert(i,v)
   • 最好的情况，i == N，不需要移动元素，即O(1)。
   • 最坏的情况，i == 0，需要移动N个元素，即O(N)。
4. remove(i)
   • 最好的情况，i == N-1，不需要移动元素，即O(1)。
   • 最坏的情况，i == 0，需要移动N个元素，即O(N)。

Fixed Space Issue 固定空间问题

紧凑数组的容量M不是无限的，它是一个有限的数值。那么这就有一个问题，在许多的应用中无法提前预知最大的容量需要多大。

• 若M过大，则未使用的空间浪费了。
• 若M过小，则没有足够的空间来存储（数组会越界）。

Variable Space 变长空间

解决方案：让M动态可变。那么当数组满了，我们生成一个更大的新数组（通常是2倍的原容量）并将旧数据移动到新数组中。那么，容量将不再成为限制，或者说只受限于计算机的内存容量（通常都很大）。
However, the classic array-based issues of space wastage and copying/shifting items overhead are still problematic.
然而，经典数组问题诸如空间浪费，复制、移动元素仍然是课题。（？没译好）

Observations 思考

对于已知可能最大元素数量的固定大小M的集合，数组已经是基于List ADT实现的合理的最佳数据结构。

对于容量为M的动态集合，由于频繁的插入、删除操作，简单的数组是一个糟糕的数据结构。
where dynamic operations such as insert/remove are common, a simple array is actually a poor choice of data structure.

Linked List 链表

现在我们介绍链表这个数据结构。它使用指针来允许元素在内存中非连续存储（这是与数组的本质区别）。元素的索引从0到N-1，使用元素i的指针来访问下一个元素i+1。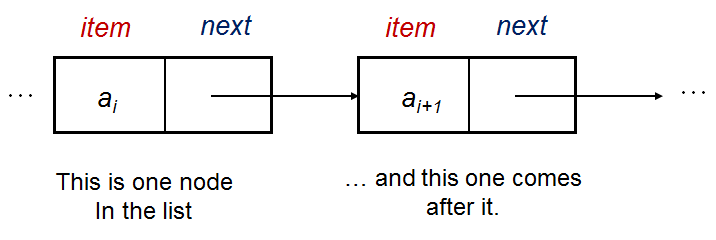

链表的C++实现

其基本形式，链表的一个单一节点包含如下结构：

struct Vertex { // we can use either C struct or C++/Java class
  int item; // the data is stored here, an integer in this example
  Vertex* next; // this pointer tells us where is the next vertex
};

Golang的实现

type Node struct {
    Item int
    next *Node
}

Linked List,Additional Data

链表这个数据结构中，还有几个额外的数据。我们使用默认的链表[22 (head)->2->77->6->43->76->89 (tail)]来说明。

1. 头节点指针指向a₀ - 它的值是22，没有谁指向头结点的。
2. 尾节点指针指向a_N-1 - 它是a₆ = 89，尾节点之后没有其他元素。

就这些，我们仅仅增加了两个额外的变量。

Variations 变化

注意在大学课本中对如何实现链表有各种细微的区别。如是否使用尾节点，是否使用循环结构，是否使用dummy head元素。discuss here

这里，我们实现的教学版本（有尾节点非循环结构，没有dummy head）可能与你所学的不是100%相同，但其核心思想是一样的。

在本教学中，每一个节点包含整型值item，但很容易更换为其他类型。

Get(i) - Much Slower than Array 比数组慢很多

由于我们保存了头尾节点的指针，除了头（索引0）尾（索引N-1）节点，其他节点需要列表顺序遍历来查找。

我们看一个简单的C++实现：

Vertex* Get(int i) { // returns the vertex
  Vertex* ptr = head; // we have to start from head
  for (int k = 0; k < i; k++) // advance forward i time(s)
    ptr = ptr->next; // the pointers are pointing to the higher index
  return ptr;
}

当i≤N-2时，其时间复杂度是O(N)。与数组的O(1)做一个比较。

Golang实现

func (ll *LL) Get(i int) *Node {
    node := ll.head
    for k:=0;k<i;k++ {
        node = node.next
    }
    return node
}

Search(v) - Not Better than Array 不比数组优

由于我们只有头尾节点的引用，另指针总是指向右侧（高位），我们只能从头结点开始，通过next指针顺序遍历。

例： [22 (head)->2->77->6->43->76->89 (tail)

在索引2处找到元素77

在列表中未找到，然而这只有在遍历完N个节点后才能确定，因此它是最坏的时间复杂度O(N)。

Insertion - Four Cases 插入的四种情况

链表的插入比数组有更多的边界条件。

大多数同学只有在它们写的链表代码失败时才能意识到所有的边界条件。

在这里，我们直接给出所有的边界。

对于插入insert(i,v)，有四种边界情况：

1. 插入链表头，i == 0。
2. 空链表（和上面的1相同）。
3. 插入尾节点之后。i == N。
4. 其他位置 i∈[1 .. N-1]。

Insert(i,v) - 头部插入(i==0)

头部插入简单高效，O(1)
C++实现如下：

Vertex* vtx = new Vertex(); // create new vertex vtx from item v
vtx->item = v;
vtx->next = head; // link this new vertex to the (old) head vertex
head = vtx; // the new vertex becomes the new head

insert(0, 50)的动画：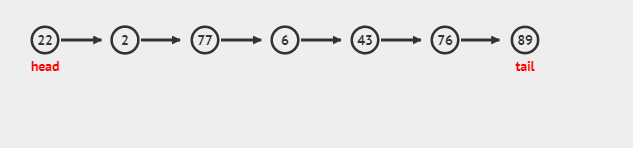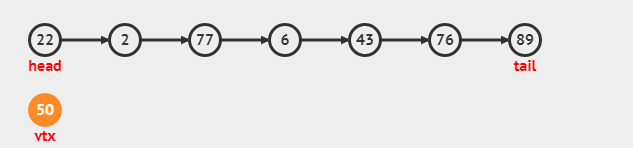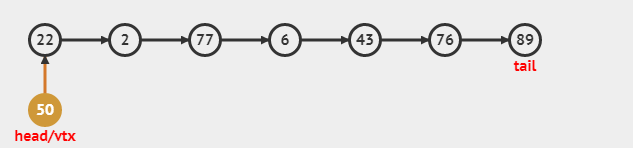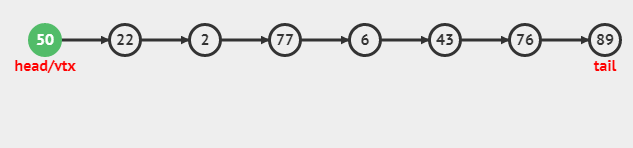

Golang实现：

node := &Node{}
node.Item = v
node.next = ll.head
ll.head = node

讨论：在数组的头部插入会发生啥？

Insert(i,v) - 插入一个空列表

空结构是一个常见的边界条件，若无何时的测试它常常导致不可预期的崩溃。向空结构中插入新元素是合法的。幸运的是，实现的伪代码和向i==0插入是一样的，因此直接使用上面的代码即可。

Insert(i,v) - i∈[1 .. N-1]

结合Get(i)的代码，我们可以实现向列表中间插入元素：

Vertex* pre = Get(i-1); // traverse to (i-1)-th vertex, O(N)
aft = pre->next; // aft cannot be null, think about it
Vertex* vtx = new Vertex(); // create new vertex
vtx->item = v;
vtx->next = aft; // link this
pre->next = vtx; // and this

Golang实现：

pre  := ll.Get(i-1)
aft  := pre.next
node := &Node{}
node.Item = v
node.next = aft
pre.next  = node

常规插入：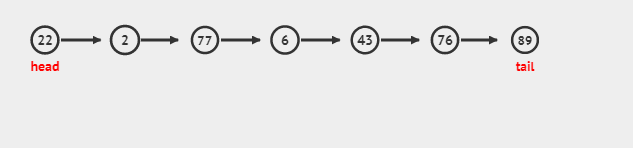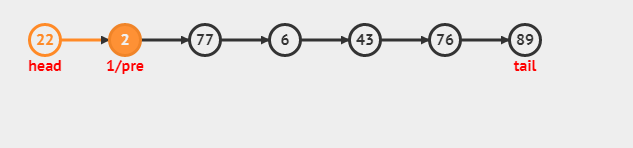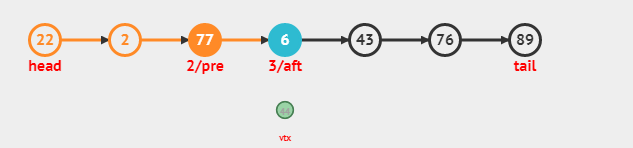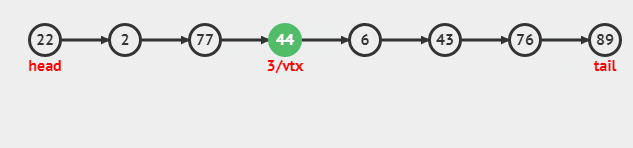

边界条件，向尾节点插入

因需要遍历列表，该操作的时间复杂度是O(N)。

Insert(i,v) - Beyond the Tail,i == N 插入尾节点之后

由于尾节点的存在，插入尾节点之后也是O(1)。

Vertex* vtx = new Vertex(); // this is also a C++ code
vtx->item = v; // create new vertex vtx from item v
tail->next = vtx; // just link this, as tail is the i = (N-1)-th item
tail = vtx; // now update the tail pointer

Golang实现:

node := &Node{}
node.Item = v
tail.next = node
tail = node

讨论：在数组的尾部之后插入会发生啥？

Removal - Three Cases 移除的三种条件

移除操作remove(i)，根据i的值有三种可能性：

1. i == 0，移除头元素，只影响head指针。
2. i == N-1，移除尾元素，只影响tail指针。
3. i ∈ [1 .. N-2]，其他位置。

讨论：对比上面的插入场景。从空结构中移除操作是否合法？

Remove(i) - At Head(i == 0) 移除头元素

非常简单，直接上代码：

if (head == NULL) return; // avoid crashing when SLL is empty
Vertex* temp = head; // so we can delete it later
head = head->next; // book keeping, update the head pointer
delete temp; // which is the old head

Golang实现：

if ll.head == nil {
  return nil
}

head := ll.head.next
ll.head = head

return head

讨论：对于数组，移除头元素会发生啥？

Remove(i) - i ∈ [1 .. N-2]

借用Get(i)的代码，很容易实现：

Vertex* pre = Get(i-1); // traverse to (i-1)-th vertex, O(N)
Vertex* del = pre->next, aft = del->next;
pre->next = aft; // bypass del
delete del;

Golang实现：

prev := ll.Get(i-1)
elem := prev.next
prev.next = elem.next

return elem

由于需要遍历列表，其时间复杂度O(N)。

Remove(i) - At Tail(i == N-1) - Part 1 移除尾元素(1)

假设列表非空，我们可以如下实现：

Vertex* pre = head;
temp = head->next;
while (temp->next != null) // while my neighbor is not the tail
  pre = pre->next, temp = temp->next;
pre->next = null; // alternatively: pre = Get(N-2), temp = Get(N-1)
delete temp; // temp = (old) tail
tail = pre; // update tail pointer

Golang实现：

pre := ll.head
temp := pre.next

for ;temp.next != nil; {
  pre = temp
  temp = temp.next
}

ll.head = pre
pre.next = nil

return temp

循环调用上述步骤，我们将从尾部逐项移除元素，直到只剩下一个元素（head == tail），此时我们再执行移除头元素的方法。注：从空结构中移除是非法的，所以当链表欧为空时，停止。

Remove(i) - At Tail(i == N-1) - Part 2 移除尾元素(2)

实际上，若我们维护了一个变量N来记录链表的大小，我们可以通过顺序遍历Get(i)来实现移除尾元素：

Vertex* pre = Get(N-2); // go to one index just before tail, O(N)
pre->next = null;
delete tail;
tail = pre; // we have access to old tail

Golang实现：

prev := ll.Get(N-2)
temp := prev.next

ll.tail = prev
prev.next = nil

return temp

注意这个操作的时间复杂度是O(N)，为了插入到尾元素之后能正常进行，需要将tail指针从N-1移动到N-2。这种不高效的做法在后面Doubly Linked List（双向链表）中解决。

讨论：对数组移除尾元素会发生啥？

时间复杂度概览

1. get(i)很慢，是O(N)。在链表中，我们需要从头元素开始顺序遍历
2. search(v)
   • 最好情况下，命中头元素，O(1)。
   • 最坏情况下，未找到，需要顺利遍历整个列表，是O(N)。
3. insert(i,v)
   • 最好情况下，插入头部，O(1)。或插入尾元素之后（有tail指针）也是O(1)。
   • 最坏情况下，插入N-2位置，我们需要顺序遍历找到元素N-2（tail的前一个元素），是O(N)。
4. remove(i)
   • 最好情况下，移除头元素，O(1)。
   • 最坏情况下，移除尾元素，为了更新tail指针需要顺序遍历整个链表，是O(N)。

链表的应用场景

单纯的线性表（顺序表）很少有应用场景，因为紧凑数组（可变长的）能做得更好。

但，链表的一个基础特性是允许元素（在内存中）非连续存储。因此是Stack栈和Queue队列的完美基础。

---

名词解释：

1. ADT